„Ha este sétáltál a hóban, akkor a reggeli latyak látványa is jobban fáj."
Nagy Anita
Véges és végtelen
Hol találkozik egymással a matematika és teológia, ha a világ megismerésében és leírásában hasonlóan gondolkodnak? Néhány elgondolkodtató modell a transzcendens és az algebrai világ kapcsolatának és egységének megragadására.
„A természettudományok és a teológia közötti kapcsolat részben azért olyan magával ragadó téma, mert sűrítve fejezi ki azt a skizofrén aggodalmat, amely a mai nyugati világot jellemzi: hogyan lehetséges, hogy egyszerre gondolkodjunk tudományosan és cselekedjünk teológiai módon; legyünk kritikusak, de ugyanakkor istentisztelők, éljünk a technológiával, de etikusan?” – idézte Wesley Wildman amerikai teológus gondolatait Kodácsy Tamás református lelkész és programozó matematikus, a KRE-ETKI Teremtésvédelmi Műhely tudományos főmunkatársa, aki Hit és tudomány: a transzcendens és az algebrai világ kapcsolata és egysége címmel tartott online előadást.
„Amikor hit és tudomány viszonyának a kérdései felmerülnek bennünk, felnőtt fejjel annak az utolsó pillanatnak a régi emlékét igyekszünk felidézni, amikor talán még egyszerre voltunk birtokában a természettudományos és a humán ismereteknek. Ez a középiskolai érettségi pillanata volt. Az akkor még meglévő szintetikus gondolkodásunkat a későbbiek során sokszor egyfajta skizofrén gondolkodásmód váltotta fel, amellyel külön látjuk ezt a két világot” – magyarázta Kodácsy. Hozzátette: általában csak a médiából értesülünk róla, hitnek és tudománynak milyen ütközőpontjai vannak, emiatt torz képünk alakul ki erről a viszonyrendszerről, amely sokkal gazdagabb és színesebb, mint hinnénk.
Két világ kapcsolata
Természettudósokkal és teológusokkal is előfordul, hogy átkalandoznak a másik területére, ilyenkor egy-egy kérdés kapcsán új modell születhet – folytatta az előadó. Ma már bőséges szakirodalma van hit és tudomány viszonyának, még magyarul is. Megjelent például a Kalligram Kiadó sorozatában Ian G. Barbour A természettudomány és a vallás találkozása – Ellenségek, idegenek vagy társak? című műve, amely alapvető tipológiát állít fel a két terület viszonyának leírására egy négyféle megközelítésből álló modell (konfliktus, függetlenség, párbeszéd és integráció) segítségével. A könyv végigveszi, mit jelent ez a négyféle megközelítés a teremtés, az evolúció, a csillagászat és más hasonló témák kapcsán.

A négyféle megközelítés közül a konfliktus a legnépszerűbb vagy legelterjedtebb, és általában ezzel találkozhatunk a médiában is. „Itt állnak szembe a tudományos materializmus konok képviselői azokkal a Bibliát szó szerint értelmező teológusokkal, akik szerint a világ csak tízezer éves. Ez a hit és tudomány viszonyának csak egy kisebb szeglete, ennél sokkal izgalmasabb és érdekesebb területek is vannak, de mivel ez szüli a legnagyobb ellenállást, ez kap nagyobb hangsúlyt a közvélekedésben is.”
A függetlenség megközelítésében mindkét terület megtalálja a maga elkülönülő tartományát, és eltérő nyelvekben és funkciókban gondolkodik. „Ennek a megközelítésnek a képviselői azt mondják, hogy ne tévedjünk egymás területére. A posztkommunista országokban az idősebb tudósok körében ez a legnépszerűbb álláspont. Egy hívő tudósnak ugyanis a kommunista rendszerben a túléléséhez hozzátartozott, hogy különválassza a hétköznapi munkáját a vasárnapi hitgyakorlástól. Ez nemcsak fizikailag, de a gondolkodásban is elkülönülést jelentett, mert ez adott biztonságot.”
A párbeszéd megközelítésében megvannak ugyan a határok, de ezek olyan határmezsgyék, amelyeket közösen kell meghatározni, és ahol a két terület kisebb átfedésekben is lehet egymással. „Ezeknek köszönhetően jó kérdéseket lehet feltenni egymásnak. Ha mindkét területre rálátunk valamennyire, akkor legalább néhány kérdést megérthetünk, még ha válaszolni nem tudunk is. Ez párhuzamokat eredményez, főleg etikai kérdésekben, de olykor olyan ontológiai kérdések kapcsán is, hogy mi az ember.”
Az integráció szintén a két terület közeledésén alapszik, de itt közös eredmények is születhetnek. Az integráció területei például a természeti teológia (natural theology), amely a középkorban is természettudományos vizsgálatokkal keresett istenbizonyítékokat. „Ez életveszélyes is lehet a teológiára nézve, hiszen az az Isten, akit a természettudományok határoznak meg, nem lesz ugyanaz, aki a zsoltárokban kijelenti magát, ezáltal elvész a személyesség. Ezzel szemben a természet teológiája (theology of nature) megpróbálja megérteni azokat a kérdéseket, amelyeket a természettudomány feltesz, és ezeknek a kérdéseknek a teológiához fűződő kapcsolatából kiindulva törekszik az integrációra.”
 Barbour tipológiája fontos viszonyítási pont mások számára is. John Haught tipológiája hasonló, de ő a konfliktus, szembenállás, érintkezés és megerősítés kategóriáit használja. Ted Peters nyolcas felosztást javasol, bár hasonló fokozatokban. Willem Drees tipológiája azt is vizsgálja, hogy a két terület hogyan fejlődött párhuzamosan és milyen tapasztalataik vannak a világról. Modelljében olyan izgalmas témák is megjelenhetnek, mint például az, hogy milyen hatással volt az európai középkorra az arab matematika térhódítása a göröggel szemben. Ekkor ugyanis olyan új, korábban megfoghatatlan fogalmak kerültek a matematikába, mint például a véletlen, az üresség, az ismeretlen vagy a végtelen.
Barbour tipológiája fontos viszonyítási pont mások számára is. John Haught tipológiája hasonló, de ő a konfliktus, szembenállás, érintkezés és megerősítés kategóriáit használja. Ted Peters nyolcas felosztást javasol, bár hasonló fokozatokban. Willem Drees tipológiája azt is vizsgálja, hogy a két terület hogyan fejlődött párhuzamosan és milyen tapasztalataik vannak a világról. Modelljében olyan izgalmas témák is megjelenhetnek, mint például az, hogy milyen hatással volt az európai középkorra az arab matematika térhódítása a göröggel szemben. Ekkor ugyanis olyan új, korábban megfoghatatlan fogalmak kerültek a matematikába, mint például a véletlen, az üresség, az ismeretlen vagy a végtelen.
Az algebra és a transzcendens
Kodácsy Tamás olyan, saját kidolgozású modellel mutatta be a két egymástól elkülönülő terület kölcsönhatásait, amely a párbeszéd és az integráció irányaiba tart, de elismeri a maga szubjektív korlátait. Arra koncentrál, hogy a világ megismerésében és leírásában milyen hasonlóságok vannak. „Mi a közös például a píben (π) és a jézusi példázatokban? Ennek megválaszolásához vissza kell mennünk eleai Zénónhoz, aki kidolgozta Akhilleusz és a teknős paradoxonát: versenyt fut Akhilleusz és a teknős, előbbi ad egy kis előnyt az utóbbinak, de amikor Akhilleusz odaér, ahonnét a teknős elindult, az már haladt valamennyit előre. Ez a végtelenségig folytatható, így a teknős egy picivel mindig Akhilleusz előtt lesz.”
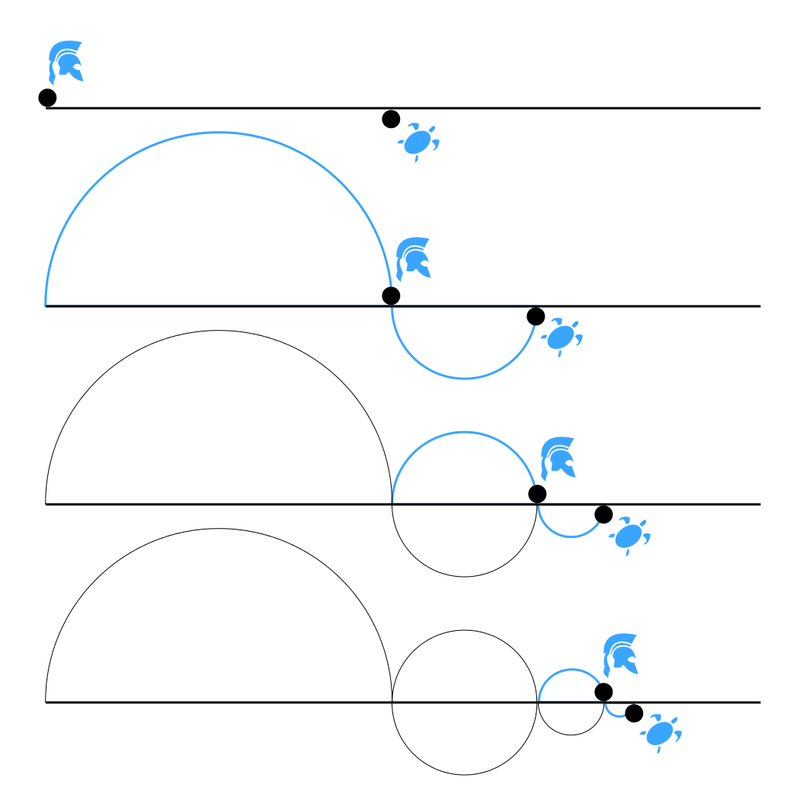 Akhilleusz távja teljes egészében tartalmazza a teknős távját. Mindketten végtelen számú ponton haladnak át, ezért a paradoxon abban áll, hogyan tartalmazhatja az egyik végtelen a másikat. „Cantor halmazelmélete szerint két halmaz elemeinek mennyiségét nemcsak úgy lehet összehasonlítani, ha külön megszámoljuk ezeket, hanem úgy is, hogy az egyik halmaz elemeit megfeleltetjük a másik halmaz elemeinek, és amelyikből marad, az a több. Ezt végtelen számosságú halmazokkal is meg tudjuk tenni, nemcsak végesekkel, és ez az izgalmas benne. Mindez akkor nevezhető kölcsönösen egyértelmű megfeleltetésnek, ha a kapcsolat egyszerre egyértelmű (injektivitás) és hézagmentes (szürjektivitás).”
Akhilleusz távja teljes egészében tartalmazza a teknős távját. Mindketten végtelen számú ponton haladnak át, ezért a paradoxon abban áll, hogyan tartalmazhatja az egyik végtelen a másikat. „Cantor halmazelmélete szerint két halmaz elemeinek mennyiségét nemcsak úgy lehet összehasonlítani, ha külön megszámoljuk ezeket, hanem úgy is, hogy az egyik halmaz elemeit megfeleltetjük a másik halmaz elemeinek, és amelyikből marad, az a több. Ezt végtelen számosságú halmazokkal is meg tudjuk tenni, nemcsak végesekkel, és ez az izgalmas benne. Mindez akkor nevezhető kölcsönösen egyértelmű megfeleltetésnek, ha a kapcsolat egyszerre egyértelmű (injektivitás) és hézagmentes (szürjektivitás).”
A teológiába Aquinói Szent Tamás hozta be a véges és végtelen fogalmát, megállapítva, hogy Isten végtelen. Véges és végtelen kapcsolatát boncolgatja az úrvacsora-tan is, amely Krisztus emberi természetéhez viszonyulva a kenyér és a bor földi, kézzel fogható jelenségét az isteni szentséghez kapcsolja. Luther szerint a véges ennek során be tudja fogadni a végtelent, Kálvin szerint viszont nem. „Ha a kölcsönösen egyértelmű megfeleltetés szempontjából nézzük, az isteni és emberi természet az injektivitásnak köszönhetően nem mosódik össze, mindkettő jelen van Krisztusban, a szürjektivitás pedig a hézagok Istenére mond nemet, azaz a mindenség létét az örökkévaló Istenben látja.”
 A Cantor-féle halmazelmélet alapján megkülönböztethetünk megszámláható számosságot és folytonos számosságot. „Mindazok a számok, amelyeket egy algebrai egyenlettel fel tudunk írni, megszámlálhatóan végtelenek. De vannak olyan algebrai számításokon kívüli számaink, amelyek számossága megszámláhatatlanul végtelen, ilyen például a pí. Ez utóbbiakat nevezik transzcendens számoknak. Az én felfogásomban a tudomány és a teológia viszonya is kicsit olyan, mint az algebrai számításokon belüli és kívüli számok egymáshoz való viszonya. Ezt a viszonyrendszert modellemben hat kategóriába sorolom.”
A Cantor-féle halmazelmélet alapján megkülönböztethetünk megszámláható számosságot és folytonos számosságot. „Mindazok a számok, amelyeket egy algebrai egyenlettel fel tudunk írni, megszámlálhatóan végtelenek. De vannak olyan algebrai számításokon kívüli számaink, amelyek számossága megszámláhatatlanul végtelen, ilyen például a pí. Ez utóbbiakat nevezik transzcendens számoknak. Az én felfogásomban a tudomány és a teológia viszonya is kicsit olyan, mint az algebrai számításokon belüli és kívüli számok egymáshoz való viszonya. Ezt a viszonyrendszert modellemben hat kategóriába sorolom.”
Az első: az egyenesnek bármilyen kis szakaszában mindig találunk algebrai és transzcendens számokat egyaránt, azaz nincs olyan szelete a valóságnak, amely megismeréséhez ne nyújtana valamit a természettudomány, és ne lenne összefüggésben valamilyen teológiai kérdéssel.
A második: az egyenesnek bármelyik kis szakaszában végtelen sok algebrai és transzcendens szám van, azaz mindkét terület képes arra, hogy a valóság egy szeletének vizsgálatakor a saját területén belül maradva mindig találjon valami újat, és felismerjen valami ismeretlent anélkül, hogy kilépne saját köréből.
A harmadik: egy új algebrai szám „felfedezése” mindig valamilyen gondolatmenet vagy az algebrai egyenletben reprezentált elv kiszámításából adódik. Azaz, ahogyan új ismeretre jutunk, építünk az előzőekre: a természettudományban például a következtetés, bizonyítás és gondolat matematikai megfogalmazása útján jutunk új ismerethez, még akkor is, ha annak megfogalmazásakor sokkal inkább az intuíció dominál.
A negyedik: amikor egy új transzcendens számot „fedezünk fel”, az vagy egy másik transzcendens számhoz kötődik, vagy tapasztalatból adódik. A teológiában a tételekhez sokkal inkább a kijelentés és tapasztalat útján jutunk, a leírás leginkább metafora, hasonlat, parabola vagy szimbólum segítségével történik.
Az ötödik: a transzcendens számokat nagyon sokszor megpróbáljuk lerövidíteni a gyakorlati alkalmazásuk során, nem píről beszélünk, hanem 3,14-ről. Sokszor a teológiában is olyan dogmák születnek a racionalizmus útján, amelyek megpróbálják algebraivá tenni a transzcendenst, és az emberek paradoxon-tűrőképességének határaihoz érve racionalizálni azt, ami nem racionális.
A hatodik: az algebrai egyenletbe bekerült transzcendens szám az egyenlet gyökét is transzcendenssé teszi. A természettudósok egyre többször ütköznek a transzcendens körébe, ilyenkor gyakran ugyanazt alkalmazzák az új tanszcendens elemekre, mint amiket saját területükön használtak. Ettől az általuk megfogalmazott teológiai gondolatmenet túlságosan szikár lesz.
Kicsit közelebb a végtelenhez
Az előadó szerint Jézus példázatai is valójában parabolák. „A parabola megpróbálja a végtelent kicsit közelebb hozni a fókuszponthoz. Amikor Jézus az Isten országáról beszél, akkor olyan hétköznapi képeket használ, amelyekben megjelenik és megmarad a transzcendencia. Megmaradnak benne a racionalitás szempontjából érthetetlen dolgok, ezeknek a megdöbbentő paradoxona továbbgondolásra ösztönöz bennünket, ezért ad ma is számtalan értelmezési lehetőséget. A példázatai nem az emberi képzelet erőfeszítéseiből merítenek, hanem Jézus Krisztus mondja nekünk őket, aki helyreállítja az istenképű embernek az istenire törekvő, de megromlott képzeletét.”
Kodácsy Tamás előadása a „Kétely, Megismerés, Bizonyosság” címet viselő online konferencián hangzott el, amelyre 2021. május 10-én került sor a Magyar Polgári Együttműködés Egyesület és a Gál Ferenc Egyetem közös szervezésében. A cikkben összefoglalt előadás teljes hosszában megtekinthető ide kattintva.
Képek: Füle Tamás, pexels.com, flickr.com